Hirotaka Problem 08

The construction described here was done with Geometer’s Sketchpad. However, it can also be done with Cabri, Geometry Expressions or GeoGebra. Anywhere where we mention ‘move the point’ we mean move the point in the dynamic geometry software environment.

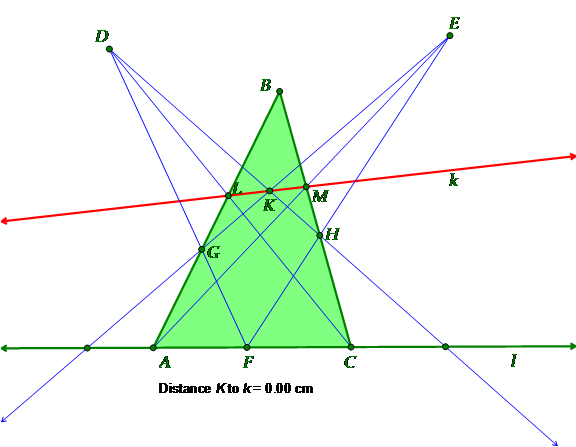
1. Draw a horizontal line and an arbitrary triangle ABC with its base on the line.
2. Select two arbitrary points D and E somewhere above the line
3. Create a point F on the base of the triangle ABC
4. Construct segment DF, label the point of intersection of it with the side of the triangle as G
5. Construct segment EF, label the point of intersection of it with the side of the triangle as H
6. Draw rays EG and DH, label intersection of these two rays as K
7. Label intersections of DC and AE with sides of the triangle as L and M
8. Construct a line k passing through the points L and M
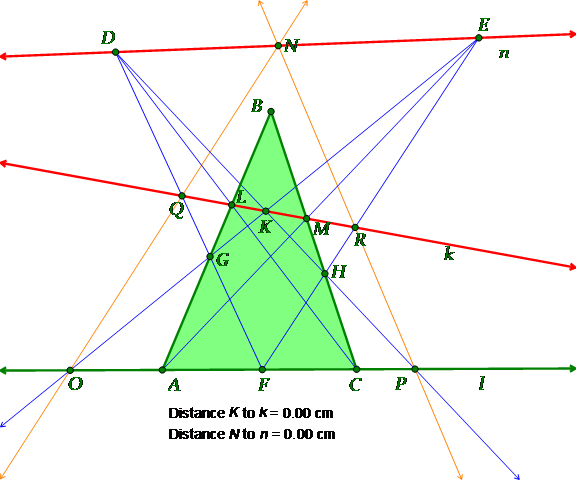
9. Calculate the distance of the line k from the point K, result is equal to 0
10. Move any of the triangle points, or any of the points D and E, the measurement d(k,K) will be still 0, this supports the claim that the three points K, L, and M are collinear.
11. PROVE that the three points K, L and M are collinear.

Continue problem 08a:

1. There are two points on the line l that were not labeled. Label them as O and P.
2. Label the point of intersection of line k with segment DF as Q
3. Label the point of intersection of line k with segment EF as R
4. Construct two lines OQ and PR, and label their intersection point as N
5. Construct line DE and label it as n. You may find that this line looks like passing through the point N.
6. Calculate the distance between the line n and point N, you should get d(n,N)=0.
7. Move any of the triangle points, or any of the points D and E, the measurement d(n,N) will be still 0, this supports the claim that the three points D, N, and E are collinear.
8. PROVE that the three points D, N and E are collinear